「ピタゴラスの定理」とは直角三角形の特徴を表した定理で「a2+b2=c2」という公式で表されますが、実は、ピタゴラスの定理はピタゴラスが発見していない可能性があることをご存知ですか。
この記事では、「ピタゴラスの定理」の意味やその活用法、証明方法や歴史などについてわかりやすく解説します。
「ピタゴラスの定理」の意味とは?

「ピタゴラスの定理」とは直角三角形の辺に関する公式
「ピタゴラスの定理」とは直角三角形の辺についての数学の公式で、「斜辺の長さの二乗は、外の辺の長さをそれぞれ二乗して足した数と同じである」という定理です。
直角三角形の斜辺を「c」として、他の辺を「a」と「b」とした場合、次のような計算式が成り立ちます。
ピタゴラスの定理は逆も成り立つ
ピタゴラスの定理は逆にしても成り立つ定理です。つまり、三角形の辺をそれぞれa、b、cとしたとき、「a2+b2=c2」の式が成り立つ三角形は、直角三角形であると言えます。これを「ピタゴラスの定理の逆」と呼びます。
ピタゴラスの定理の別称は「三平方の定理」
ピタゴラスの定理は「三平方の定理」と呼ばれることもあります。「三平方の定理」という名称は、第二次世界大戦中に敵語である英語の使用を禁じられていたために発案された呼び名です。数学者の末綱恕一(すえつなじょいち)によって考案されました。
ピタゴラスの定理は中3の数学で学ぶ
ピタゴラスの定理は中学3年生の数学で学びます。ピタゴラスの定理の意味を習い、典型的な問題として、直角三角形の3辺のうち2辺の長さがわかっている場合の残りの1辺の長さを求める問題がよく出題されます。
「ピタゴラスの定理」は何に使うのか?

「ピタゴラスの定理」の建築設計で使われる
「ピタゴラスの定理」は中学数学で学んだあとは役に立たないと思っている方もいるかもしれませんが、「ピタゴラスの定理」は実用的に使われています。
例えば、建築設計で斜面の長さを計算するときにピタゴラスの定理が使われます。屋根の幅と高さからピタゴラスの定理を使って斜面の長さを算出して、斜面に使われる部材の長さを割り出します。
カーナビにもピタゴラスの定理が使われている
また、カーナビを搭載している車の位置を正確に割り出すために、ピタゴラスの定理が活用されています。
車の位置の割り出し方は、まず車から発信される電波を衛星が受け取るまでの時間から車と衛生までの距離を算出します。同時に、衛星は地球までの最短距離を測り、衛星から地球に最も近い地上の地点と車、衛星の3点で直角三角形を作りピタゴラスの定理を用いて車の正確な位置を割り出すのです。
ピタゴラスの定理を応用して星までの距離を測定
ピタゴラスの定理の応用例に「三角測量の原理」があります。「三角測量」とは地上の3点を結んで三角形を作り、そのうちの1辺の長さを測定し、それを基準にほかの2辺の長さや頂点にあたる位置を求めていく方法です。
この三角測量の原理を使えば、地球からある一定の星までの距離を測定することができます。太陽を中心に地球は公転しているので、夏の地球の位置から見える星の角度と、太陽をはさんで真逆にある冬の地球の位置から測定したい星の角度が同じです。その角度と、地球から太陽までの距離を使って星までの距離を割り出します。
ピタゴラスの定理の証明方法とは?

ピタゴラスの定理の証明方法は100種類以上
ピタゴラスの定理はこれまでに100種類以上の方法で証明されてきました。例えば、直角三角形ABCの直角になる頂点から斜辺に垂線を伸ばして全部で3つの相似の関係にある三角形から証明する方法や、相似と半円を使って証明する方法などがあります。
ユークリッドのピタゴラスの定理の証明
数学者ユークリッドは著書『原論』のなかで、ピタゴラスの定理を3つの正方形を使って証明しました。
直角三角形の各辺を1辺とした正方形を三角形の外側に記します。ここに記された3つの正方形の面積を使いながらピタゴラスの定理を証明するのですが、複雑な計算式を使わずに、図形を駆使しながら証明していくことで有名です。
正方形を使った証明
直角三角形を4つ用意した証明方法もあります。同じ大きさの直角三角形ABCを4つ用意して、その直角を利用して正方形を作ります。すると、その中に正方形が一つと、直角三角形の外側にできる大きな正方形ができます。
それらの正方形の面積と4つの直角三角形の面積を使ってピタゴラスの定理を証明します。
「ピタゴラスの定理」の歴史

ピタゴラス以外が発見したという説が有力
「ピタゴラスの定理」は、紀元前540年頃にエーゲ海のサモス島出身の数学者ピタゴラスによって発見されたと言われています。そのため「ピタゴラスの定理」と名付けられたのですが、本当にピタゴラスがこの定理をしたかどうかはわかっていません。
5世紀にプロクロスの著作『ユークリッド原論注釈』や紀元前1世紀に著されたウィトルウィウスの『建築十書』には「ピタゴラスの定理」という記述がありますが、ユークリッド自身はピタゴラスの定理を証明したときには「ピタゴラス」という言葉を使っていません。つまり、ユークリッドがピタゴラスの定理を証明したときには「ピタゴラスの定理」とは名付けられていなかった可能性があります。
ピタゴラス以前に残る「ピタゴラスの定理」の記述
その一方で、紀元前1800年頃に書かれたとされるバビロニア数学を記録した粘土板『プリンプトン322』には「ピタゴラスの定理」と同内容の記述が残されています。この粘土板はピタゴラスが生まれる以前に作られていますので、ピタゴラスの定理はピタゴラスが生まれる以前にすでに発見されていたと考えられます。
「ピタゴラスの定理」の英語表現
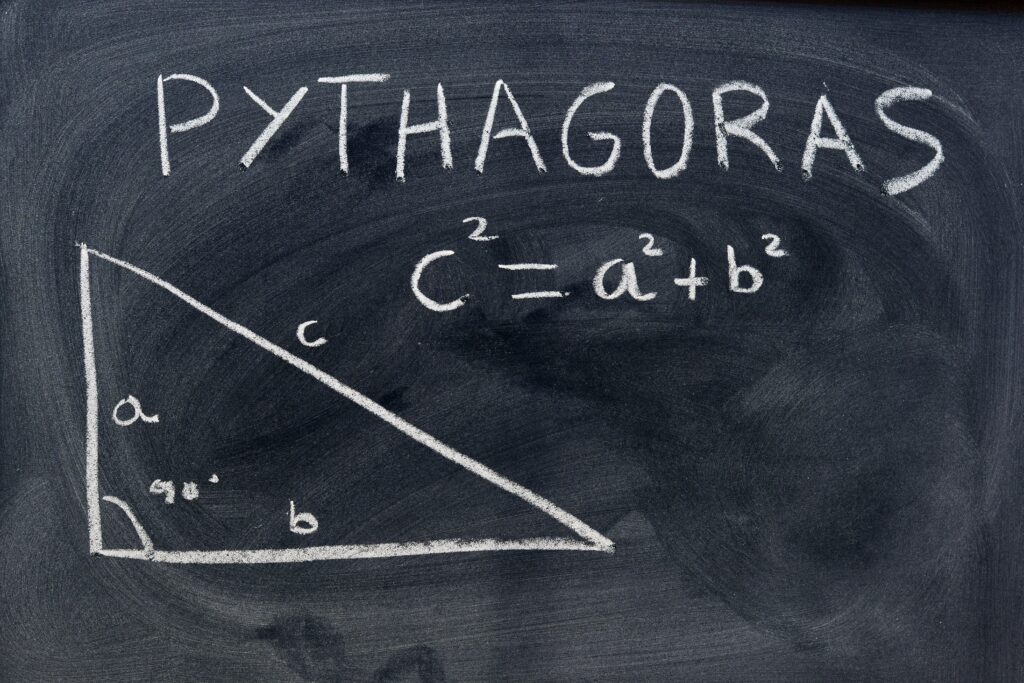
「ピタゴラスの定理」は英語で「Pythagorean theorem」
「ピタゴラスの定理」は英語で「the Pythagorean theorem」で、「Pythagorean」の頭文字「P」は大文字にします。
また「ピタゴラスの定理の逆」は「the converse of the Pythagorean theorem」です。
「ピタゴラスの定理」の英語例文
- “He tried to prove the Pythagorean theorem.”
「彼はピタゴラスの定理の証明を試みた」 - “She uses Pythagorean theorem to measure the distance to a star.”
「彼女はピタゴラスの定理を使って星までの距離を測定する」
まとめ
「ピタゴラスの定理」とは直角三角形の斜面の長さの2乗した数が、残りの各辺の長さを二乗した数の和と同じになるという定理です。100以上の証明方法がある有名な定理なのですが、同時にピタゴラスが発見したのかどうかがわからないという謎が残された定理でもあります。





a2+b2=c2